Download Word (docx):

Navigate using audio

End of chapter 3 / Beginning of chapter 4

Anouncements

  • Going over the clicker question from last class

Schrodinger Wave Equation

  • Audio 0:01:46.280749

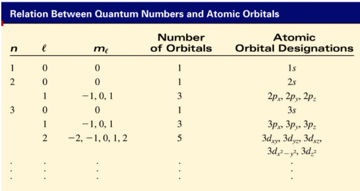
What are the allowed values of quantum numbers?

  • Audio 0:02:40.811261

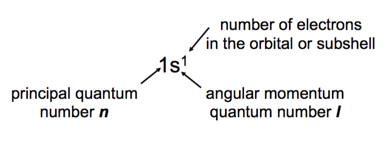
Schrodinger Wave Equation Ψ = fn(n, l, ml, ms)

  • Ψ = fn(n, l, ml, ms)
  • principal quantum number n
  • n = 1, 2, 3, 4, ….
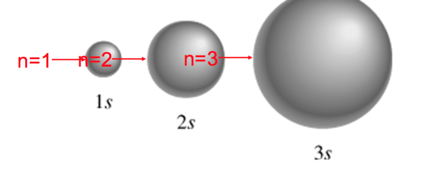
  • Audio 0:05:02.318180
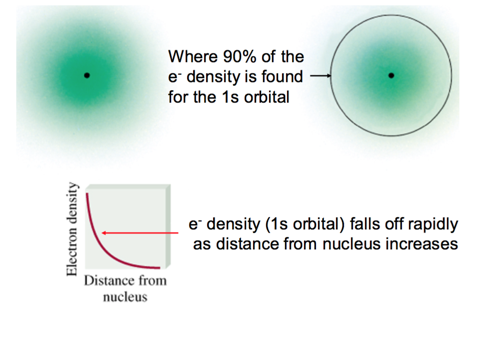
  • You are trying to find where the electron probably
  • The sphere is 90% chance of where you can find the electron

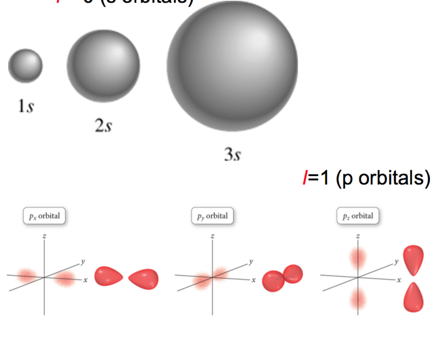
The l quantum number

  • Audio 0:07:39.803509
  • controls shape of the space the electron can occupy

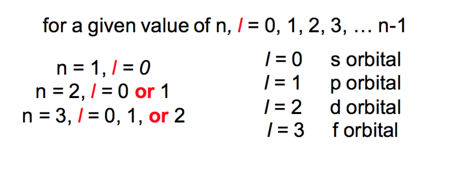
l = 0 (s orbitals)

l = 2 (d orbitals)

  • Audio 0:09:58.512569
  • Audio 0:12:02.335350
  • There are many orientations for different orbital shapes.
    • For l = 1 (dumbell), you have three m_l orientations
    • For l = 2 (four balloons), 5 different orientations

Schrodinger Wave Equation

  • Audio 0:14:45.362121
  • Ψ= fn(n, l, ml, ms)
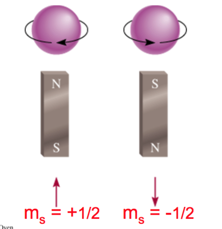
  • spin quantum number ms
  • ms = +1/2 or -1/2
  • Stern-Gerlach
  • Audio 0:15:13.028156
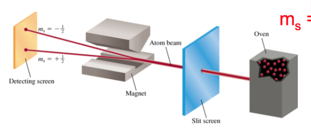
  • Audio 0:16:48.075265

Clicker question

  • Audio 0:18:00.445172
  • Electrons in an orbital with l = 2 are in a/an?
    • A) d orbital

Question 2

  • Audio 0:18:38.887100
  • How many orbitals are allowed in a sublevel if the angular momentum quantum number for electrons in that sublevel is 3
    • If l = 3 what are possible m_l’s
    • 7

Question 3

  • What is the maximum number of electrons in a atom that can have the following set of quantum numbers?
    • 1
    • Audio 0:22:52.890279

Probability & Radial Distribution Functions

  • Audio 0:23:12.640771
  • Ψ2 is the probability density
    • the probability of finding an electron at a particular point in space
    • for s orbital: maximum at the nucleus?
    • decreases as you move away from the nucleus
  • the Radial Distribution function represents the total probability at a certain distance from the nucleus
    • maximum at most probable radius
  • nodes in the functions are where the probability drops to 0

Two Dimensional Standing wave with radial nodes

  • Audio 0:28:08.691820

2s and 3s

  • Audio 0:29:43.309772
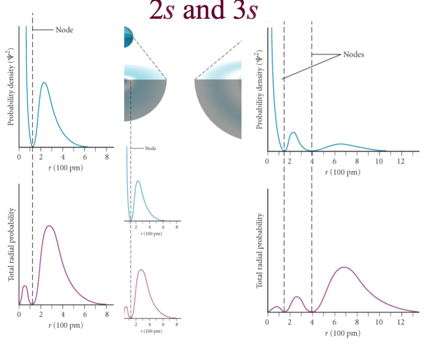
  • Difference between probability density and the radial density

Chapter 4 - Periodic Properties of the Elements

  • Audio 0:31:36.612589

  • How do we add electrons to orbitals?

Schrodinger Wave Equation

  • Audio 0:32:21.264224
  • Ψ= fn(n, l, ml, ms)
  • Existence (and energy) of electron in atom is described by its unique wave function Ψ.
  • Pauli exclusion principle - no two electrons in an atom can have the same four quantum numbers.

  • Audio 0:34:53.838546

Schrodinger Wave Equation

  • Shell – electrons with the same value of n
  • Subshell – electrons with the same values of n and l
  • Orbital – electrons with the same values of n, l, and ml
  • How many electrons can an orbital hold?
    • If n,l,and ml are fixed,then ms =1/2or-1/2 Ψ= (n, l, ml, 1/2)orΨ= (n, l, ml, -1/2)
    • An orbital can hold 2 electrons
  • Audio 0:36:43.265603
  • How many 2p orbitals are there in an atom?

Clicker 3

    • B

Energy of orbitals in a single electron atom

  • Audio 0:39:54.807493
  • Energy only depends on principle quantum number n

Coulomb’s Law

  • Audio 0:41:07.948707
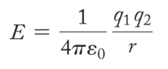
  • Coulomb’s law describes the attractions and repulsions between charged particles.
    • For like charges, the potential energy (E) is positive and decreases as the particles get farther apart as r increases.
    • For opposite charges, the potential energy is negative and becomes more negative as the particles get closer together.
    • The strength of the interaction increases as the size of the charges increases.
      • Electrons are more strongly attracted to a nucleus with a 2+ charge than to a nucleus with a 1+ charge.

Penetration & Shielding

  • Audio 0:42:15.187414
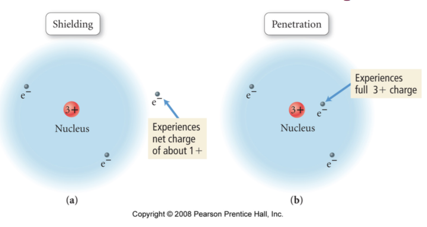
  • Audio 0:43:45.128001
  • From radial distribution function: 2s orbital penetrates more deeply
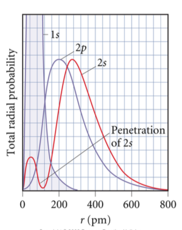    • into 1s orbital than does 2p
  • the weaker penetration => electrons in the 2p sublevel experience more repulsive force & are more shielded from nucleus (less attractive force)
  • =>electrons in 2s sublevel lower E than in 2p
  • Penetration causes the energies of sublevels in the same principal level to not be degenerate.
  • In the fourth and fifth principal levels, the effects of penetration become so important that the s orbital lies lower in energy than the d orbitals of the previous principal level.
  • The energy separations between one set of orbitals and the next become smaller beyond the 4s orbital.
    • The ordering can therefore vary among elements, causing variations in the electron configurations of the transition metals and their ions.

General Energy Ordering of Orbitals for Multi-electron Atoms

  • Audio 0:45:59.121493

Electron configurations

  • Electron configuration is how the electrons are distributed among the various atomic orbitals in an atom.

Vocab

Term Definition
nodes parts of a probability density function where probability drops to zero
unique electrons’ existence in an atom is _
Pauli exclusion principle Says no two electrons in an atom can have the same four quantum numbers
shell electrons with the same value of n are in the same _
subshell electrons with the same values of n and l are in the same _
orbital electrons with the same values of n, l, and ml are in the same _
Coulomb’s law says opposite charges attract and same charges repel
electron configuration how electrons are distributed among the various atomic orbitals in an atom