Clicker 1

• A sample of NI3 is contained in a piston and cylinder. The samples rapidly decomposes to form nitrogen gas and iodine gas, and releases 3.30 kJ of heat and does 950 J of work. What is ∆E?
  • A) -953.3 J
  • B) +953.3 J
  • C) -4250 J
  • D) -946.7 J
  • E) +4250 J

C

Exchanging Energy between System and Surroundings

• Exchange of heat energy
  • q = mass × specific heat × ΔTemperature
• Exchange of work
  • w = −Pressure × ΔVolume
  • 

Measuring ΔE: Calorimetry at Constant Volume

• Because ΔE = q + w, ΔE can be determined by measuring q and w.
• In practice, it is easiest to do a process in such a way that there is no change in volume, so w = 0.
  • At constant volume, ΔEsystem = qsystem.
• In practice, temperature changes of individual chemicals involved in the reaction cannot be observed directly, so instead the temperature change in the surroundings is measured.
  • Using an insulated container (e.g., controlled surroundings)
  • qsystem = −qsurroundings
• The surrounding area is called a bomb calorimeter and is usually made of a sealed, insulated container filled with water.
  • qsurroundings = qcalorimeter = –qsystem

Bomb Calorimeter

• 
• It is used to measure ΔE because it is a constant volume system.
• The heat capacity of the calorimeter is the amount of heat absorbed by the calorimeter for each degree rise in temperature and is called the calorimeter constant.
  • Ccal, kJ/°C

Practice Problem: Measuring ΔErxn in a Bomb Calorimeter

• When 1.010 g of sucrose (C12H22O11) undergoes combustion in a bomb calorimeter, the temperature rises from 24.92 oC to 28.33 oC. Find ΔErxn for the combustion of sucrose (in kJ/mol). The heat capacity of the calorimeter is 4.90 kJ/oC.

Clicker 2

• A 35.6 g sample of ethanol (C2H5OH) is burned in a bomb calorimeter, according to the following reaction. If the temperature rose from 35.0 to 76.0°C and the heat capacity of the calorimeter is 23.3 kJ/°C, what is the value of ΔErxn? The molar mass of ethanol is 46.07 g/mol.
  • C2H5OH(l) + 3 O2(g) → 2 CO2(g) + 3 H2O(g) ΔErxn = ?
  • A) -1.24 × 103 kJ/mol
  • B) +1.24 × 103 kJ/mol
  • C) -8.09 × 103 kJ/mol
  • D) -9.55 × 103 kJ/mol
  • E) +9.55 × 103 kJ/mol

A

Enthalpy: Heat Evolved at Constant Pressure

• “Bomb” Calorimetry is nice but…. we would like to work at atmospheric pressure
• For a system at e.g. atmospheric pressure the total energy is E plus the energy required to push the gas aside to make space for the system: PV
• The enthalpy, H, of a system is the sum of the internal energy of the system and the product of pressure and volume.
  • H is a state function.
    • H = E + PV
• The enthalpy change, ΔH, of a reaction is the heat evolved in a reaction at constant pressure.
  • ΔHreaction = qreaction at constant pressure
• Usually ΔH and ΔE are similar in value; the difference is largest for reactions that produce or use large quantities of gas.

Endothermic and Exothermic Reactions

• When ΔH is negative, heat is being released by the system into the surroundings.
  • The surroundings will “feel” hot.
  • Temperature of the surroundings increased from the energy released by the system.
  • This is called an exothermic reaction.
• When ΔH is positive, heat is being absorbed by the system from the surroundings.
  • The surroundings will “feel” cold.
• Temperature of the surroundings decreased because energy left the surroundings to flow into the system.
• This is called an endothermic reaction.

Particulate View of Exothermic Reactions

• For an exothermic reaction, the surrounding’s temperature rises due to a release of thermal energy by the reaction.
• This extra thermal energy comes from the conversion of some of the chemical potential energy in the reactants into kinetic energy in the form of heat.
• During the course of a reaction, existing bonds are broken and new bonds are made.
• The products of the reaction have less chemical potential energy than the reactants.
• The difference in energy is released as heat.

Particulate View of Endothermic Reactions

• In an endothermic reaction, the surrounding’s temperature drops due to absorption of some of its thermal energy by the reaction.
• During the course of a reaction, existing bonds are broken and new bonds are made.
• The products of the reaction have more chemical potential energy than the reactants.
• To acquire this extra energy, some of the thermal energy of the surroundings is converted into chemical potential energy stored in the products.

Enthalpy of Chemical Reaction

• The enthalpy change in a chemical reaction is an extensive property.
  • The more reactants you use, the larger the enthalpy change.
• By convention, we calculate the enthalpy change for the number of moles of reactants in the reaction as written. C3H8(g) + 5 O2(g) → 3 CO2(g) + 4 H2O(g) ΔH = −2044 kJ 1 mol C3H8(g) = –2044 kJ or 5 mol O2(g) = –2044 kJ

Practice Problem: Enthalpy Stoichiometry

• Calculate the heat (in kJ) associated with the complete combustion of all of the propane in a 13.2 kg propane tank: C3H8(g) + 5O2(g) è 3CO2(g) + 4H2O(g) ΔHrxn= -2044 kJ

Measuring ΔH: Calorimetry at Constant Pressure

• Reactions done in aqueous solution are at constant pressure.
• The calorimeter is often nested foam cups containing the solution.
  • qreaction = –qsolution = –(masssolution × Cs, solution × ΔT)
• ΔHreaction = qconstant pressure = qreaction
  • To get ΔHreaction per mol, divide by the number of moles.
• 

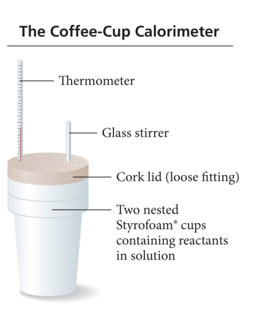
Practice Problem: Calorimetry Magnesium metal reacts with hydrochloric acid:

• Mg(s) + 2HCl(aq) –> MgCl2 + H2(g) you combine 0.158 g of Mg with enough HCl to make 100.0 mL of solution in a coffee-cup calorimeter. T of the solution rises from 25.6 oC to 32.8 oC. Find ΔHrxn, assume density of solution is 1.00g/ml

Vocab

Term	Definition
bomb calorimeter	used to measure ΔE because it is a constant volume system
calorimeter constant	the amount of heat absorbed by the calorimeter for each degree rise in temperature (capacity)
enthalpy (H)	the sum of the internal energy of the system and the product of pressure and volume