Week 14 - Day 3
Clicker 1
- Use the standard reaction enthalpies given below to determine ΔH°rxn for the following reaction 2 NO(g) + O2(g) → 2 NO2(g) ΔH°rxn = ?
- Given:
- N2(g) + O2(g) → 2 NO(g) ΔH°rxn = +183 kJ
- 1/2 N2(g) + O2(g) → NO2(g) ΔH°rxn = +33 kJ
- A) -150. kJ
- B) -117 kJ
- C) -333 kJ
- D) +115 kJ
- E) +238 kJ
- Given:
Standard Conditions and Standard Enthalpy of Formation (ΔHf)
- Audio 0:00:21.144316
- The standard state is the state of a material at a defined set of conditions.
- Pure gas at exactly 1 atm pressure
- Pure solid or liquid in its most stable form at exactly 1 atm pressure and temperature of interest
- Usually 25 °C
- Substance in a solution with concentration 1 M
- The standard enthalpy change, ΔH°, is the enthalpy change when all reactants and products are in their standard states.
- Audio 0:02:59.978786
- The standard enthalpy of formation, ΔH°f, is the enthalpy change for the reaction forming 1 mole of a pure compound from its constituent elements.
- The elements must be in their standard states.
- The ΔHf° for a pure element in its standard state = 0 kJ/mol.
Table of Standard Enthalpies (ΔHf)
- Audio 0:05:22.505566
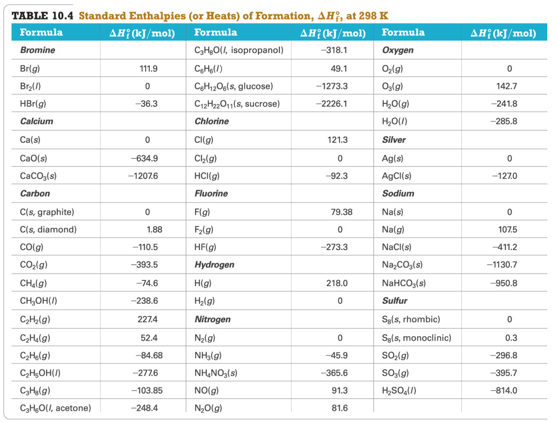
Practice Problem: Standard Enthalpies of Formation (ΔHf)
- Audio 0:08:11.763970
- Write the appropriate equations for the heats of formation of MgCO3(s) and C6H12O6(s)
Clicker 2
- The standard enthalpy of formation (ΔHo f) for potassium chloride is the enthalpy change for the reaction:
- A) K(g) + ½Cl2(g) è KCl(g)
- B) K+(g) + Cl- (g) è KCl(s)
- C) 2K(s) + Cl2(g) è 2KCl(s)
- D) K(s) + ½Cl2(g) è KCl(s)
- E) K+(g) + Cl- (g) è KCl(g)
Calculating Standard Enthalpy Change for a Reaction
- Audio 0:12:36.053007
- Any reaction can be written as the sum of formation reactions (or the reverse of formation reactions) for the reactants and products.
- The ΔH° for the reaction is then the sum of the ΔHf° for the component reactions. ΔH° reaction = ∑nΔHf °(products) − ∑nΔHf °(reactants) ∑ means sum. n is the stoichiometric coefficient of the reaction.
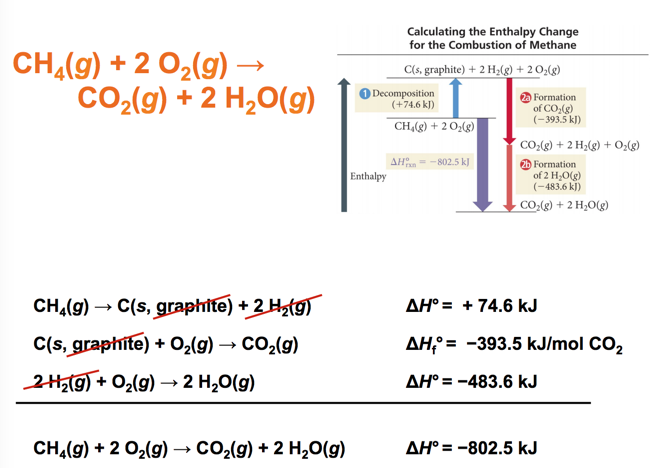
CH4(g) + 2 O2(g) → CO2(g) + 2H2O(g)
- C(s, graphite) + 2 H2(g) → CH4(g) ΔHf°= − 74.6 kJ/mol CH4
- C(s, graphite) + O2(g) → CO2(g) ΔHf°= −393.5 kJ/mol CO2
- H2(g) + ½ O2(g) → H2O(g) ΔHf° = −241.8 kJ/mol H2O
CH4(g) + 2 O2(g) → CO2(g) + 2H2O(g)
- Audio 0:17:54.502946

Practice Problem: Standard Enthalpies of Formation (ΔHf )
- Audio 0:18:40.315050
- What is the change in enthalpy for the reaction 4NH3(g) + 5O2(g) è 4NO(g) + 6H2O(g)
Clicker 3
- Audio 0:21:26.032462
- Use the ΔH°f information provided to calculate ΔH°rxn for the following SO2Cl2(g) + 2 H2O(l) → 2 HCl(g) + H2SO4(l) ΔH°rxn = ?
- ΔH° f (kJ/mol)
- SO2Cl2(g) -364
- H2O(l) -286
- HCl(g) -92
- H2SO4(l) -814
- A) -256 kJ
- B) +161 kJ
- C) -62 kJ
- D) +800. kJ
- E) -422 kJ
Ionic Bonding and the Crystal Lattice
- Audio 0:26:20.219643
- The extra energy that is released comes from the formation of a structure in which every cation is surrounded by anions, and vice versa.
- This structure is called a crystal lattice.
- The crystal lattice is held together by the electrostatic attraction of the cations for all the surrounding anions.
- The crystal lattice maximizes the attractions between cations and anions, leading to the most stable arrangement.
Lattice Energy
- The extra stability that accompanies the formation of the crystal lattice is measured as the lattice energy.
- The lattice energy is the energy released when the solid crystal forms from separate ions in the gas state.
- Always exothermic
- Hard to measure directly, but can be calculated from knowledge of other processes
- Lattice energy depends directly on the size of charges and inversely on distance between ions.
Determining Lattice Energy: The Born–Haber Cycle
- The Born–Haber cycle is a hypothetical series of reactions that represents the formation of an ionic compound from its constituent elements.
- The reactions are chosen so that the change in enthalpy of each reaction is known except for the last one, which is the lattice energy.
Born–Haber Cycle and Hess’s Law
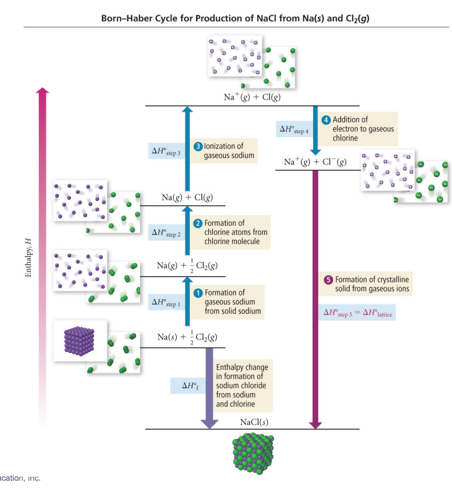
- Use Hess’s law to add up enthalpy changes of other reactions to determine the lattice energy.

Trends in Lattice Energy: Ion Size
- Audio 0:31:13.639819
- The force of attraction between charged particles is inversely proportional to the distance between them.
- Larger ions mean the center of positive charge (nucleus of the cation) is farther away from the negative charge (electrons of the anion).
- Larger ion = weaker attraction
- Weaker attraction = smaller lattice energy
Lattice Energy versus Ion Size
- Audio 0:31:57.501608
- The force of attraction between oppositely charged particles is directly proportional to the product of the charges.
- Larger charge means the ions are more strongly attracted.
- Larger charge = stronger attraction
- Stronger attraction = larger lattice energy
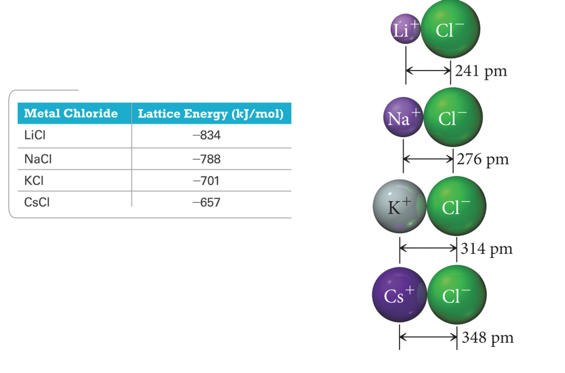
Trends in Lattice Energy: Ion Charge
- The force of attraction between oppositely charged particles is directly proportional to the product of the charges.
- Larger charge means the ions are more strongly attracted.
- Larger charge = stronger attraction
- Stronger attraction = larger lattice energy
- Of the two factors, ion charge is generally more important.

Which compound should have the largest lattice energy?
Ch 11
- What is a Gas?
Vocab
| Term | Definition |
|---|---|
| bond energy | amount of energy it takes to break one mole of a bond in a compound |
| standard state | state of a material at a defined set of conditions |
| standard enthalpy change (ΔH°) | the enthalpy change when all reactants and products are in their standard states |
| standard enthalpy of formation (ΔH°f) | the enthalpy change for the reaction forming 1 mole of a pure compound from its constituent elements |
| Born–Haber cycle | a hypothetical series of reactions that represents the formation of an ionic compound from its constituent elements |