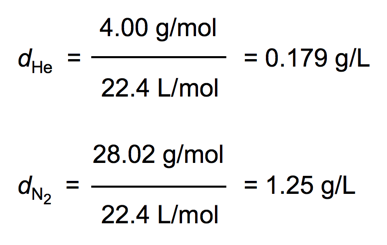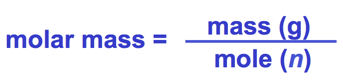Download Word (docx):

Navigate using audio

Final

  • Week from today
  • Slightly more weighted toward things on ch 10 and 11
  • Review session
    • 2 - 4:30 Saturday and Sunday after next
      • review sessions in Shelby hall

  • Final is 11:30 - 2

  • Liquid nitrogen experiment

Clicker 1

  • Audio 0:06:15.196390
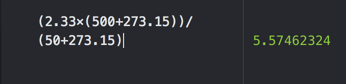
  • To what volume will a sample of gas expand if it is heated from 50.0 C and 2.33 L to 500.0 C?
    • A) 5.57 L
    • B) 23.3 L
    • C) 0.233 L
    • D) 0.97 L
    • E) 0.184 L

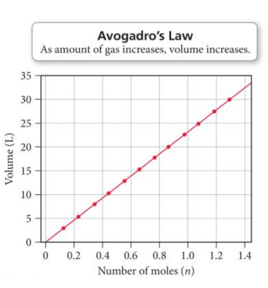
Avogadroʼs Law: Volume and Moles Have a Direct Relationship

  • Audio 0:11:31.193983
  • Volume is directly proportional to the number of gas molecules when pressure and temperature are held constant. – More gas molecules = larger volume
  • Equal volumes of gases contain equal numbers of molecules. – The gas doesn’t matter.
  • V = constant × n (moles)
  • V/n = constant
  • (V1/n1) = (V2/n2)
  • The volume of a gas sample increases linearly with the number of moles of gas in the sample.

Clicker 2

  • Audio 0:14:23.279569
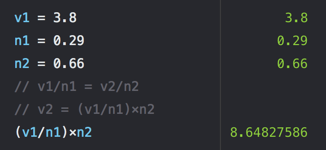
  • If a sample of 0.29 moles of Ar occupies 3.8 L under certain conditions, what volume will 0.66 moles occupy under the same conditions?
    • A) 12
    • B) 8.6
    • C) 17
    • D) 5.0
    • E) 15

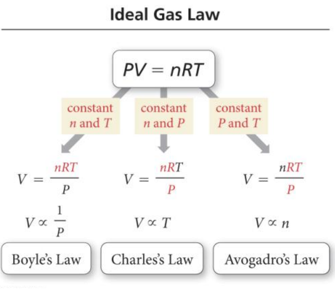
Ideal Gas Law: PV = nRT

  • Audio 0:17:10.738500
  • The simple gas law relationships discussed so far can be combined into a single law that encompasses all of them.
    • V α (1/P) Boyle’s Law
    • V α T Charles’s Law
    • V α n Avogadro’s Law
  • Ideal gas law: PV = nRT – Where
    • P is pressure in atm
    • V is volume in liters
    • n is moles
    • R is the ideal gas law constant, 0.0821 (L · atm)/(K · mol) – T is temperature in kelvins

Ideal Gas Law: PV = nRT

  • Audio 0:18:31.572724
  • · The other gas laws are found in the ideal gas law if two variables are kept constant. · The ideal gas law allows us to find one of the variables if we know the other three.

Practice Problem: Ideal Gas Law

  • Audio 0:19:52.714114
  • Calculate the volume occupied by 0.845 mol of nitrogen gas at a pressure of 1.37 atm and temperature of 42 °C

Practice Problem: Ideal Gas Law

  • Audio 0:22:41.752192

  • Calculate the number of moles of gas in a 3.24 L basketball inflated to a total pressure of 24.3 psi

Standard Conditions

  • Audio 0:26:03.240956
  • Because the volume of a gas varies with pressure and temperature, chemists have agreed on a set of conditions to report our measurements so that comparison is easy. – These are called standard conditions (STP).
  • Standard pressure = 1 atm
  • Standard temperature = 273 K = 0 °C
  • Standard amount = 1 mol
  • Standard volume = 22.4 L – The volume occupied by one mole of a substance is its molar volume at STP (T = 273 K or 0 °C and P = 1atm).

Molar Volume at STP

  • Audio 0:28:15.214651
  • The volume of one mole of gas at STP is called the molar volume.
    • 6.022 × 1023 molecules of gas – Note that the type of gas is immaterial.
  • It is important to recognize that one-mole measures of different gases have different masses, even though they have the same volume.

Density of a Gas

  • Audio 0:29:06.988437
  • Density is the ratio of mass to volume. – Density = (mass/volume)
  • Density of a gas is generally given in grams/liter (g/L).
  • The mass of 1 mol = molar mass.
  • The volume of 1 mol at STP = 22.4 L.
    • Density (d) = [mass of gas (g/mol)]/[volume (L)]
      • Density (g/L) = (molar mass)/(molar volume)

Density of a Gas at STP

  • Audio 0:29:33.594188
  • For example, the densities of helium and nitrogen gas at STP are as follows:

Molar Mass of a Gas

  • Audio 0:30:27.999878
  • One of the methods chemists use to determine the molar mass of an unknown substance is to heat a weighed sample until it becomes a gas; measure the temperature, pressure, and volume; and use the ideal gas law.

Gas Density

  • Audio 0:31:34.143033
  • PV = nRT

Gas Density

  • Audio 0:34:08.137349

Practice Problem: Density of a Gas

  • Audio 0:34:25.383706
  • A sample of gas has a mass of 0.311 g. Its volume is 0.225 L at 55 oC and pressure of 886 mmHg. What is the molar mass?

Mixtures of Gases and Partial Pressures

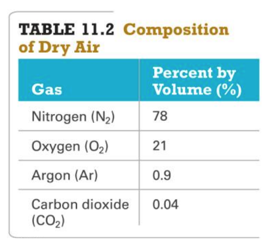
  • Many gas samples are not pure but are mixtures of gases.
  • Dry air, for example, is a mixture containing nitrogen, oxygen, argon, carbon dioxide, and a few other gases in trace amounts.
  • Therefore, in certain applications, the mixture can be thought of as one gas. – By knowing air’s pressure, volume, and temperature, the total moles of molecules in an air sample can be determined—even though they are different compounds.

Partial Pressure: Pgas

  • Audio 0:38:48.952989
  • The pressure of a single gas in a mixture of gases is called its partial pressure.
  • The partial pressure of a gas can be calculated if – a fraction of the mixture it composes and the total pressure are known; or – the number of moles of the gas in a container of a given volume and temperature are known.
  • The sum of the partial pressures of all the gases in the mixture equals the total pressure. This is known as Daltonʼs law of partial pressures.
    • Ptotal = Pa + Pb + Pc + …
  • Gases behave independently.

Partial Pressure: Pgas

  • Audio 0:40:46.362349
  • The pressure due to any individual component in a gas mixture is its partial pressure (Pn).
  • The partial pressure from the ideal gas law can be determined by assuming that each gas component acts independently.
    • RT Pn = nn V

Vocab

Term Definition
relationship between volume and moles V = constant * n(moles)
standard conditions Using these conditions 22.4 L is the volume of one mol of any gas (1 atm, 273 K (0 C), 1 mol)
partial pressure the pressure of a single gas in a mixture of gases
Daltonʼs law of partial pressures Ptotal = Pa + Pb + Pc + …